日本在线电影一区二区三区_午夜视频体内射.COM.COM_人妻体体内射精一区二区

欢迎您访问【千度】hfqszs.com-aaaaaa级特色特黄的毛片,青青河边草高清免费,美女MM131爽爽爽,日韩欧美一区二区三区免费看

看見函數(shù)軟件0.11.6 安卓最新版全站導(dǎo)航最近更新

戰(zhàn)壕戰(zhàn)爭1914國際版(Trench Warfare1914) 像素風(fēng)策略戰(zhàn)爭游戲
網(wǎng)易光遇手游正版點亮星空共慶周年
地鐵跑酷體驗服國際服all stars 地鐵跑酷體驗服版本
六花軟件庫app手機(jī)安卓吧超多軟件各種版本資源隨意下載。
李跳跳自動跳廣告MissLee 幫你自動跳廣告

歷史搜索

首頁 → 安卓軟件 → 教育學(xué)習(xí) → 看見函數(shù)軟件 0.11.6 安卓最新版

看見函數(shù)軟件0.11.6 安卓最新版

大小：14.9M

時間：2021-11-24 11:56

星級：

語言：中文

環(huán)境：Android

版本：0.11.6 安卓最新版

類別：國產(chǎn)軟件/ 免費軟件

官網(wǎng)：暫無

廠商：

軟件介紹軟件截圖相關(guān)下載相關(guān)文章評論(0)

精品下載精心為您推薦：

編輯點評：可以在手機(jī)上畫出函數(shù)的工具

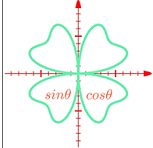
在手機(jī)上繪制函數(shù)的工具，看見函數(shù)app的功能很強(qiáng)大，支持平面曲線，空間曲線，曲面，函數(shù)又包含了普通方程，極坐標(biāo)方程，參數(shù)方程多種內(nèi)容，簡單好用又實用的工具，畫函數(shù)必備。

看見函數(shù)軟件

功能介紹

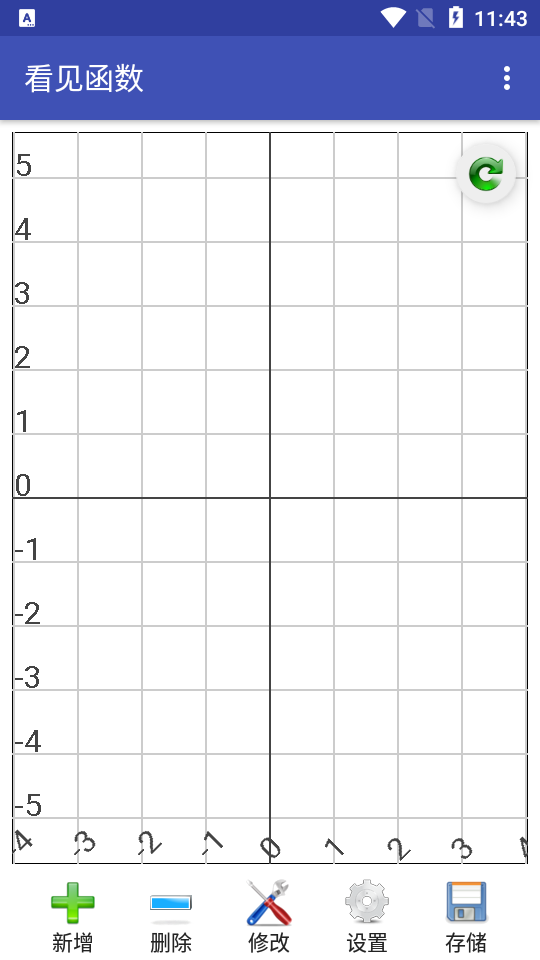
1、平面曲線

2、平面曲線（可變參）

3、空間曲線

4、曲面

5、曲面可變參）

6、個性化推薦

幫助說明

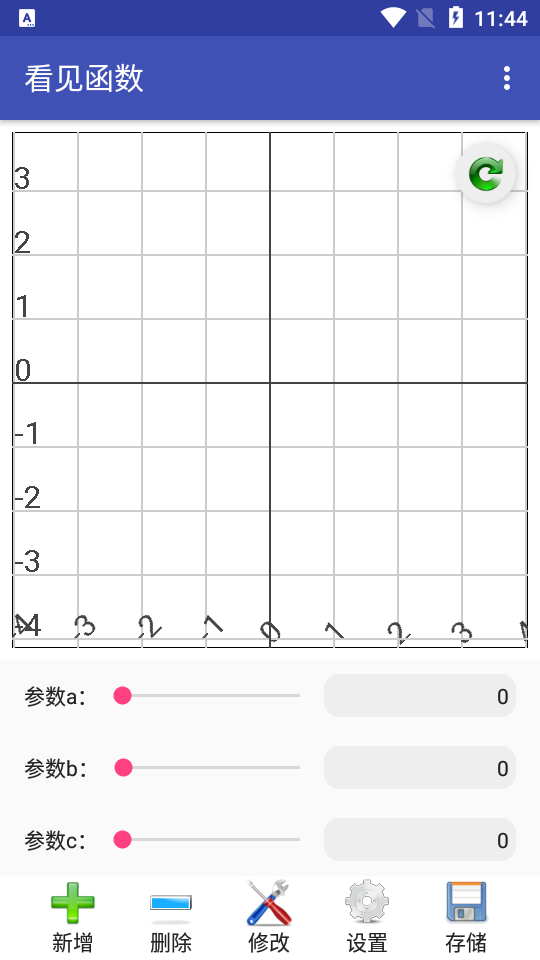
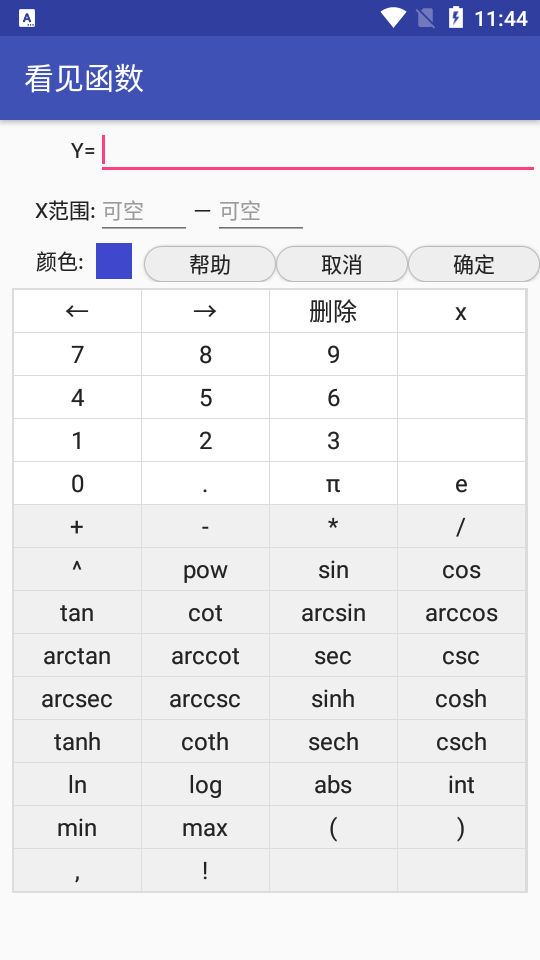
x：變量

a:可變參數(shù)a

b：可變參數(shù)b

c:可變參數(shù)c

注意：乘號不能省略，如3sin(x)

要寫成3*sin(x)；cos(Tx)要寫成

coS(TT*X)

+：加法

-：減法

*：乘法

/：除法

：冪函數(shù)或指數(shù)函數(shù)。例如x的開方為x~（1/2)；3的x的指數(shù)為3~x

！：階乘。僅支持非負(fù)整數(shù)，如果是小

數(shù)則先四舍五入然后再計算階乘

pow：與相同。例如x的1.5的冪為pow(x,1.5)；3的x的指數(shù)為pow(3,x)

pow：與相同。例如x的1.5的冪為

pow(x,1.5)；3的x的指數(shù)為pow(3,x)

sin：正弦函數(shù)，寫法為sin(x)

cos：余弦函數(shù)，寫法為cos(x)

tan:正切函數(shù)，寫法為tan(x)

cot：余切函數(shù)，寫法為cot(x)

arcsin：反正弦函數(shù)，寫法為arcsin(x)

arccos：反余弦函數(shù)，寫法為arccos(x)

arctan:反正切函數(shù)，寫法為arctan(x)

arccot：反余切函數(shù)，寫法為arccot(x)

sec:正割函數(shù)，寫法為sec(x)

csc:余割函數(shù)，寫法為csc(x)

arcsec:反正割函數(shù)，寫法為arcsec(x)

arccsc：反余割函數(shù)，寫法為arccsc(x)

sinh：雙曲正弦函數(shù)，寫法為sinh(x)

cosh：雙曲余弦函數(shù)，寫法為cosh(x)

tanh：雙曲正切函數(shù)，寫法為tanh(x)

coth：雙曲余切函數(shù)，寫法為coth(x)

sech：雙曲正割函數(shù)，寫法為sech(x)

csch：雙曲余割函數(shù)，寫法為csch(×)

In：自然對數(shù)，寫法為In(x)。其他對數(shù)請用換底公式

log：常用對數(shù)，寫法為log(×)。其他對數(shù)請用換底公式

abs：絕對值，寫法為abs(x)

min：最小值，寫法為min(3,x)

max：最大值，寫法為max(1.7,x)

int：取整，寫法為int(x)

軟件特色

根據(jù)用戶輸入的一元函數(shù)繪制函數(shù)曲線，根據(jù)用戶輸入的二元函數(shù)繪制函數(shù)曲面，根據(jù)用戶輸入的帶可變參數(shù)的函數(shù)繪制曲線，根據(jù)用戶輸入的帶可變參數(shù)的函數(shù)繪制曲面，根據(jù)用戶輸入的方程繪制三維曲線。

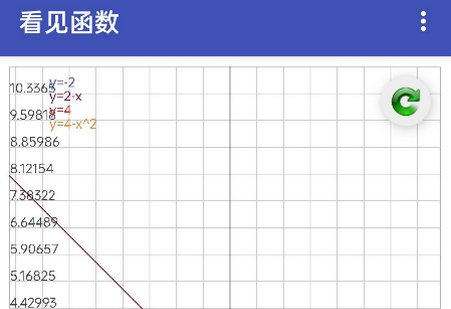
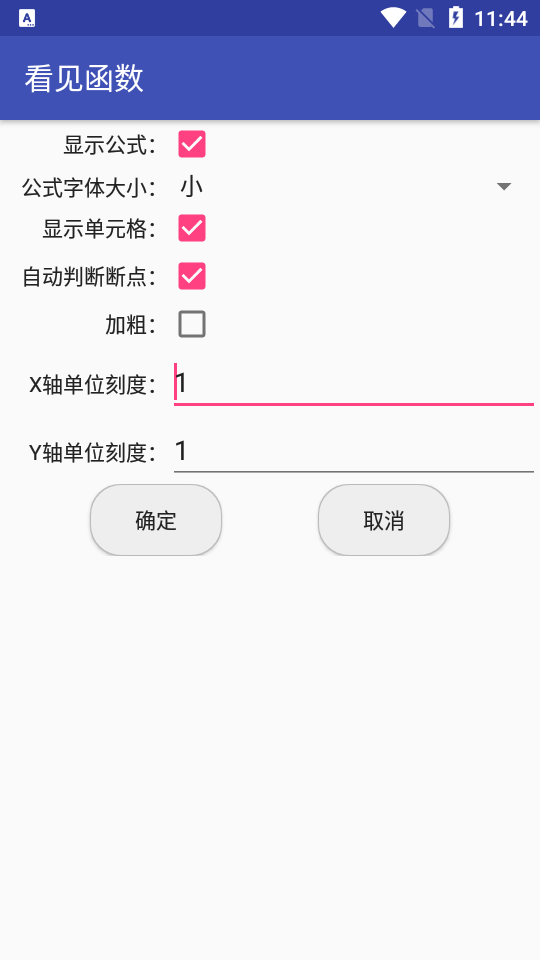
對于平面曲線，可以進(jìn)行位移和縮放操作，可以同時繪制多個函數(shù)的曲線，每條曲線的顏色可以設(shè)置；

看見函數(shù)軟件

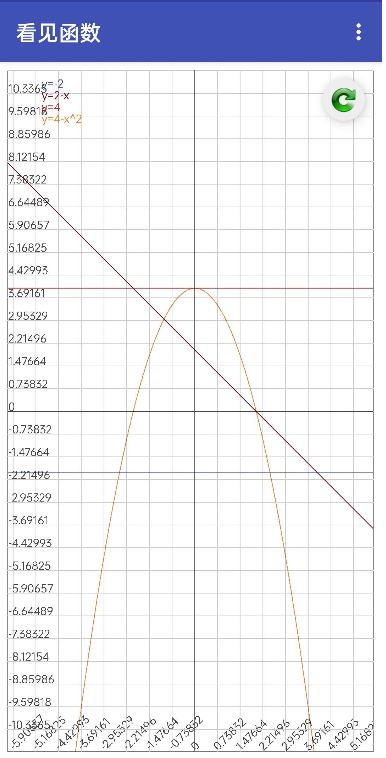
對于曲面可以進(jìn)行調(diào)整視角和觀察空間；

對于帶可變參數(shù)的曲線和曲面，可以手動調(diào)節(jié)參數(shù)觀察函數(shù)曲線或曲面的變化。

支持冪函數(shù)、指數(shù)函數(shù)、對數(shù)函數(shù)、三角函數(shù)等所有初等函數(shù)。

可以保存輸入的函數(shù)，也可以重新加載保存的函數(shù)。

擴(kuò)展閱讀

函數(shù)（function），最早由中國清代數(shù)學(xué)家李善蘭翻譯，出自他的《代數(shù)》一書。他之所以這樣翻譯，是因為“此變量中的每個人都是彼此的函數(shù)”，也就是說，函數(shù)是指隨另一個數(shù)量的變化而變化的數(shù)量，或一個包含另一個數(shù)量的數(shù)量。函數(shù)的定義通常分為傳統(tǒng)定義和現(xiàn)代定義。函數(shù)的兩個定義基本相同，只是敘述概念的起點不同。傳統(tǒng)定義是從運動變化的角度來看的，現(xiàn)代定義是從集合和映射的角度來看的。

功能的起源

中國數(shù)學(xué)書籍中使用的“功能”一詞是翻譯詞。是中國數(shù)學(xué)家李善蘭在翻譯“代數(shù)”時（1859年）將“功能”翻譯成“功能”。

在中國古代，“字母”與“包含”一詞相同，兩者均具有“包含”的含義。李善蘭給出的定義是：“流派包含了天空的功能。”中國古代使用天空，地球，人和物這四個詞來代表4個不同的未知數(shù)或變量。該定義的含義是：“只要公式包含變量x，該公式就稱為x的函數(shù)。”因此，“函數(shù)”是指公式中變量的含義。我們指的方程式的確切定義是指包含未知數(shù)的方程式。但是，在我國早期的數(shù)學(xué)專著《九章算術(shù)》中，術(shù)語方程是指包含多個未知量的同時線性方程，即一組線性方程。