欢迎您访问【千度】hfqszs.com-aaaaaa级特色特黄的毛片,青青河边草高清免费,美女MM131爽爽爽,日韩欧美一区二区三区免费看

三角函數計算器手機版v1.0 安卓版 全站導航最近更新

  • 戰壕戰爭1914國際版(Trench Warfare1914) 像素風策略戰爭游戲
  • 網易光遇手游正版 點亮星空共慶周年
  • 地鐵跑酷體驗服國際服all stars 地鐵跑酷體驗服版本
  • 六花軟件庫app手機安卓吧 超多軟件各種版本資源隨意下載。
  • 李跳跳自動跳廣告MissLee 幫你自動跳廣告
歷史搜索

熱門搜索：冒險島楓之傳說手游黎明覺醒生機騰訊正版攜程旅行app手機版地鐵跑酷手游國服逃跑吧少年官方版

首頁 → 安卓軟件 → 工具其它 → 三角函數計算器手機版 v1.0 安卓版
三角函數計算器手機版圖標

三角函數計算器手機版v1.0 安卓版

  • 大小：33.2M
  • 時間：2024-01-19 16:09
  • 星級：
  • 語言：中文
  • 環境：Android
  • 版本：v1.0 安卓版
  • 類別：國產軟件/ 免費軟件
  • 官網：暫無
  • 廠商：武漢柒號教室科技有限公司

軟件介紹 軟件截圖 相關下載 相關文章 評論(0)

精品下載精心為您推薦：

編輯點評：計算三角函數的工具

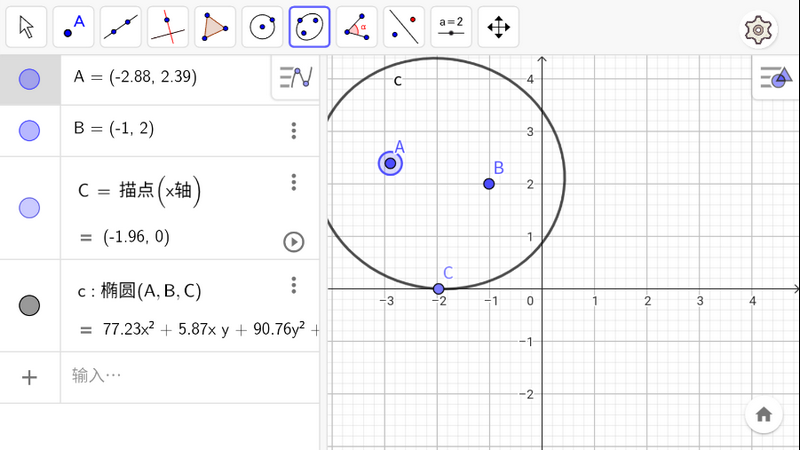
三角函數計算器是一款功能強大的數學工具，它不僅可以繪制函數、方程、零值點和極值點，還可以求導數和積分。此外，它還可以幫助用戶構造及分析多邊形、圓、圓錐曲線和其他軌跡，創建動態幾何構圖。無論是繪制函數、隱式方程、極坐標曲線還是參數曲線，都可以在這款App中輕松完成。

三角函數計算器手機版

三角函數計算器App怎么樣

三角函數計算器App不僅包含了基本的三角函數計算，還提供了求導數、積分、構造和分析多種類型的回歸等功能。并且實用性強，無論是在學習還是工作中，都能幫助用戶快速解決各種數學問題。

三角函數計算器App的功能

1. 繪制函數和方程，輸入函數或方程，自動繪制出對應的圖形。

2. 求導數和積分：輸入函數或方程，App會計算出其導數和積分。

3. 構造和分析多種類型的回歸：可以輸入一組數據，App會構造出最適合這組數據的回歸模型。

三角函數計算器使用教程

1. 打開App，選擇需要的功能，如“繪制函數”或“求導數”。

三角函數計算器手機版

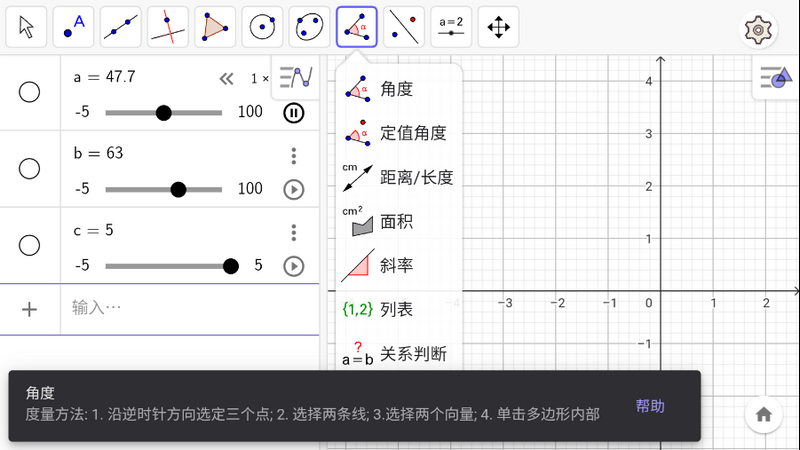
2. 根據提示輸入相應的信息，如函數表達式或數據。

三角函數計算器手機版

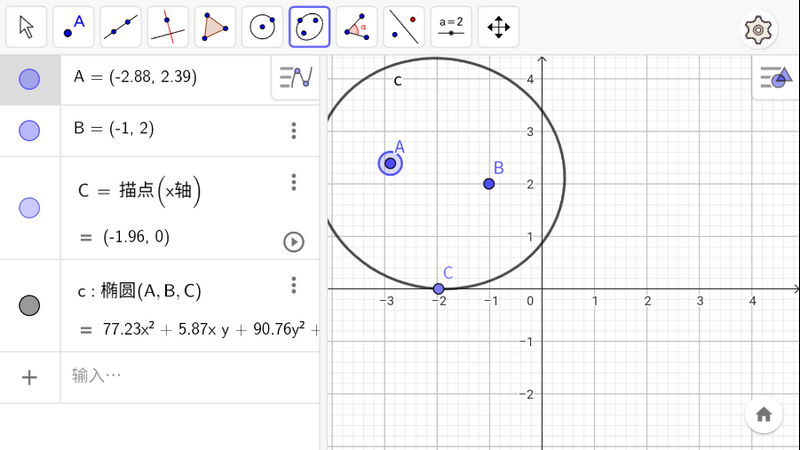
3. App會自動進行計算并顯示出結果。

三角函數計算器手機版

軟件點評

三角函數計算器App是一款非常實用的數學工具，它的功能強大，操作簡單，無論是學生還是教師，都能從中受益。特別是對于學習三角函數的學生來說，這款App無疑是最好的學習助手。

什么是三角函數？

三角函數是數學中屬于初等函數中的超越函數的一類函數，它們的本質是任何角的集合與一個比值的集合的變量之間的映射。最常見的三角函數包括正弦、余弦和正切，這些函數均是在平面直角坐標系中定義的，其定義域為整個實數域。

在具體的應用方面，三角函數在研究三角形和圓等幾何形狀的性質時有重要作用，也是研究周期性現象的基礎數學工具。比如，正弦、余弦和正切是直角三角形邊長的比，可以用來計算角度和邊長。

不僅如此，三角函數也在數學分析中有廣泛的應用。例如，三角函數可以被定義為無窮級數或特定微分方程的解，允許它們的取值擴展到任意實數值，甚至是復數值。盡管三角函數公式看似很多、很復雜，但只要掌握了三角函數的本質及內部規律，就會發現三角函數各個公式之間有強大的聯系。

三角函數的計算方法

三角函數的計算方法有很多種。首先，對于一些特殊的角度如30°，45°，60°，15°，75°等，我們可以通過一些初等三角學結論簡單地算出。例如，一個等邊三角形的每個內角都是60°，如果知道等腰三角形底邊對應的高、中線與角平分線重合，就可以推導出相關的三角函數值。

此外，還有一些重要的積化和差公式、和差化積公式、倍角半角公式可以使用。例如，我們知道 sin(2kπ + α) = sinα ， cos(2kπ + α) = cosα 等公式，其中k為整數。

然后，還需要記住一些誘導公式，比如當π+α的三角函數值與α的三角函數值之間的關系：sin(π+α) = -sinα，cos(π+α) = -cosα等。

最后，對于一些復雜的角度或者需要精確計算的情況，我們可以使用計算器。在線計算器或數學軟件中，你可以輸入角度和要求解的三角函數類型（正弦、余弦、正切等），然后得到準確的結果。

三角函數計算器手機版截圖

下載地址

    網友評論

    熱門評論

    最新評論

    發表評論查看所有評論(0)

    昵稱:
    表情: 高興 可 汗 我不要 害羞 好 送花 親親
    字數: 0/500 (您的評論需要經過審核才能顯示)

    TOP榜

    亚洲色在线无码国产精品| 久久精品人| 丁香五月成人影院|