編輯點評:2021新高考數學一輪復習真題和模擬題匯編pdf
2021高考數學一輪復習真題和模擬題匯編優秀專題匯總由精品小編整理并分享,歡迎老師同學們下載并閱讀。如果對你有幫助,請繼續支持查看哦
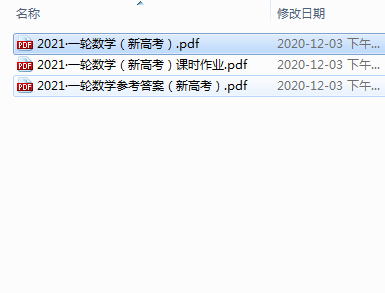
2021數學一輪復習大綱
高考數學一輪復習計劃開始的時間從8月就開始了。為什么呢?因為這個時候你的中考錄取結果已經知道,也已經放松了一個多月,是時候開始進入新學期的狀態,投入到新的高中生活中了。
高考數學一輪復習時間
第一輪復習從今年8月開始到明年3月中旬,大約用時7個月左右,采用的的是地毯式轟炸,章節復習,不留任何知識死角,追求全面性、基礎性,是同學們鞏固基礎,提高認識的重要階段。許多以前成績不好的同學就是利用一輪復習成績得以突飛猛進的,可以說兩輪復習中最重要最關鍵的是第一輪復習!
高考數學一輪復習目標
1、抓住重點內容。高中數學里函數(含三角函數)、平面向量、直線和圓錐曲線、線面關系、數列、概率、導數等知識,是每年的必考點,要把他們當做重中之重去復習,在復習過程中一個一個專題去落實,每個知識點都吃透,掌握好解題方法和技巧。
2、拓實基礎。高考對基礎知識考察比較全面,而且也是突出重點來考察,所以,在新一輪復習階段,一定要把教材復習到位,對教材中的概念、公式、法則、定理的形成要重視,不要覺得自己已經掌握了就不花時間來鞏固,當你真的認真去看的時候,可能會發現,原來這個定理書上是有的,自己沒有注意到,回歸到書本的基礎知識和理論,拓實基礎,在第一輪復習很重要。
3、養成答題好習慣。在復習階段重要的部分是各種校考模擬考,計算和邏輯推理是數學考察的兩大方面,在復習階段,除了要復習鞏固知識,還應該通過各種訓練方式,來提高和規范運算能力和邏輯推理能力,學生可以找一些難題或者經典的考題來專項訓練,大量的訓練和思考。
高考數學一輪復習注意事項
1、必須強調的是,制訂計劃必須按自己的特點自己制訂,不能仿制別人的計劃,別人告訴你的方法最多是個參考,不能完全套用的。只有自己去試著做,摸索出自己的完整方法,才是有用的。
2、別把你的時間安排得太緊。計算時間要精確,但你也得為在最后一分鐘冒出來的問題留下解決的時間。制訂一份生活計劃,而不僅僅制訂一份學習計劃。生活是多方面的,你必須認清它的多面性。
3、要有足夠的睡眠時間。醫學研究證實每人每天必須有八小時的睡眠。我們應該清楚這一點,即學習質量的好壞取決于是否有足夠的睡眠。
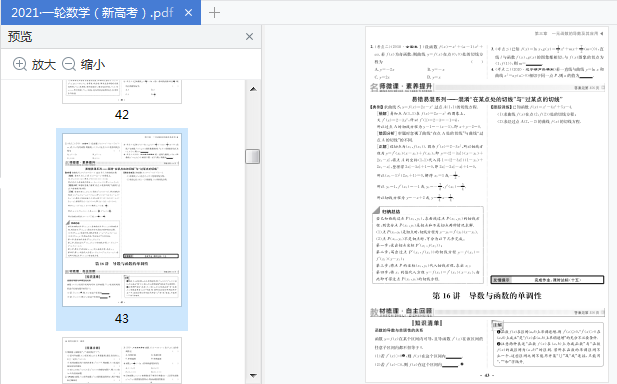
相關內容部分預覽
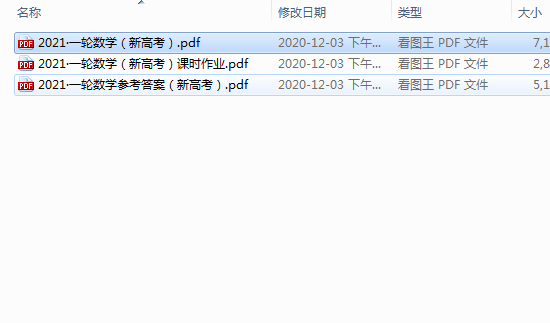






21個解題方法和100個高頻考點大整理
網上有個段子,有人問:數學是什么?
回答:數學就是,授之以魚,考之以鱈 鰹 漁 鰾 鰳 鰳 鰻 鰻 鳘 鰵。
授人以魚不如授人以漁?
老師第一個不答應,明明可以既授人以魚,又授人以漁呀!
今天的文章,高考數學的高頻考點(魚)和解題技巧(漁)都給你,一輪復習的同學,趕快收藏起來。
【需要打印版,可下拉至文末獲取。】
中數學解題的21個典型方法與技巧
1、解決絕對值問題(化簡、求值、方程、不等式、函數)的基本思路是:把絕對值的問題轉化為不含絕對值的問題。具體轉化方法有:
①分類討論法:根據絕對值符號中的數或表達式的正、零、負分情況去掉絕對值。
②零點分段討論法:適用于含一個字母的多個絕對值的情況。
③兩邊平方法:適用于兩邊非負的方程或不等式。
④幾何意義法:適用于有明顯幾何意義的情況。
2、根據項數選擇方法和按照一般步驟是順利進行因式分解的重要技巧。因式分解的一般步驟是:提取公因式→選擇用公式→十字相乘法→分組分解法→拆項添項法。
3、利用完全平方式把一個式子或部分化為完全平方式就是配方法,它是數學中的重要方法和技巧。配方法的主要根據有:
4、解某些復雜的特型方程要用到換元法。換元法解題的一般步驟是:設元→換元→解元→還元。
5、待定系數法是在已知對象形式的條件下求對象的一種方法。適用于求解點的坐標、函數解析式、曲線方程等重要問題的解決。其步驟是:
①設
②列
③解
④寫
6、復雜代數等式條件的使用技巧:右邊化為零,左邊變形。
10、代數式求值的方法有:①直接代入法②化簡代入法③適當變形法(和積代入法)。注意:當求值的代數式是字母的“對稱式”時,通常可以化為字母“和與積”的形式,從而用和積代入法求值。
11、方程中除未知數以外,含有的其他字母叫做參數,這種方程叫做含參方程。解含參方程一般要用“分類討論法”,其原則是:①按照類型求解②根據需要討論③分類寫出結論。
17、一元二次不等式的解法:一元二次不等式可以用因式分解法求解。簡便的實用解法是根據“三個二次”間的關系,利用二次函數圖像去解。具體步驟如下:
二次系數化為正→判別且求根→畫出示意圖→解集橫軸中
18、一元二次方程根的討論:一元二次方程根的符號問題或m型問題可以利用根的判別式和根與系數的關系來解決,但根的一般問題、特別是區間根的問題要根據“三個二次”間的關系,利用二次函數圖像去解。一般思路:題意→二次函數圖像→不等式組(a的符號、△的情況、對稱軸的位置、區間端點函數值的符號)。
19、基本函數在區間上的值域:①定義域沒有特別限制時---記憶法或結論法;②定義域有特別限制時---圖像截斷法,即畫出圖像→截出一段→得出結論
20、最值型應用題的解法:解決最值型應用題的基本思路是函數方程法,其解題步驟是:設變量→列函數→求最值→寫結論
21、穿線法是解高次不等式和分式不等式的最好方法。其一般思路是:首項系數化為正→求根標根→右上起穿→奇穿偶回。注意:①高次不等式首先要用移項和因式分解的方法化為“左邊乘積、右邊是零”的形式。②分式不等式一般不能用兩邊都乘以公分母的方法來解,要通過移項、同分合并、因式分解的方法化為“商零式”,用穿線法解。

 2021年二建水利通關藍寶書
2021年二建水利通關藍寶書 2021年二建市政通關藍寶書在線閱讀
2021年二建市政通關藍寶書在線閱讀 2022考蟲數學高數必練1000題pdf
2022考蟲數學高數必練1000題pdf 黃岡歷年中考物理試卷及答案解析2007-2020年整合版
黃岡歷年中考物理試卷及答案解析2007-2020年整合版 黃岡市中考化學試卷2012-2020年整合版
黃岡市中考化學試卷2012-2020年整合版 黃岡中考英語試卷及答案2007-2020整合word版
黃岡中考英語試卷及答案2007-2020整合word版 黃岡數學中考試卷及答案2011-2020年整合版
黃岡數學中考試卷及答案2011-2020年整合版 計算機畢業設計:ASP語言設計完整版
計算機畢業設計:ASP語言設計完整版 2021年中國95后女性洞察報告pdf免費在線閱讀
2021年中國95后女性洞察報告pdf免費在線閱讀 中國減貧學報告電子版免費在線閱讀
中國減貧學報告電子版免費在線閱讀

















 黃岡歷年中考試題及答案解析2012-2020年語文試卷word無水印版
黃岡歷年中考試題及答案解析2012-2020年語文試卷word無水印版 幼兒園綜合素質學習筆記pdf電子版完整版
幼兒園綜合素質學習筆記pdf電子版完整版 幼兒園保教知識與能力學習筆記pdf電子版免費版
幼兒園保教知識與能力學習筆記pdf電子版免費版 小學教育教學知識與能力學習筆記電子版手寫板
小學教育教學知識與能力學習筆記電子版手寫板 中學綜合素質學習筆記在線閱讀完整版
中學綜合素質學習筆記在線閱讀完整版 中學教育知識與能力學習筆記pdf電子版免費版
中學教育知識與能力學習筆記pdf電子版免費版 專插本英語詞匯必備3400pdf完整版
專插本英語詞匯必備3400pdf完整版 廣東省專插本必刷2000題政治理論答案電子版免費版
廣東省專插本必刷2000題政治理論答案電子版免費版 2020全國中考物理真題及答案解析合集免費版
2020全國中考物理真題及答案解析合集免費版 2020全國中考英語真題試卷及答案解析整合版
2020全國中考英語真題試卷及答案解析整合版 2020全國中考數學真題試卷及答案解析匯總大全docx可打印版
2020全國中考數學真題試卷及答案解析匯總大全docx可打印版 2020全國中考語文真題及解析匯總整合版免費版docx完整版
2020全國中考語文真題及解析匯總整合版免費版docx完整版 數學物理方程講義完整版1-5講電子版pdf高清無水印版
數學物理方程講義完整版1-5講電子版pdf高清無水印版 大小: 33.3M
大小: 33.3M













 中考復習資料大全
中考復習資料大全 三年級復習資料合集
三年級復習資料合集 二級建造師考試資料大全
二級建造師考試資料大全 數學題庫文檔
數學題庫文檔 十二校聯合教育學基礎第三版筆記和課后習題pdf免費版
十二校聯合教育學基礎第三版筆記和課后習題pdf免費版
熱門評論
最新評論
發表評論查看所有評論(0)