欢迎您访问【千度】hfqszs.com-aaaaaa级特色特黄的毛片,青青河边草高清免费,美女MM131爽爽爽,日韩欧美一区二区三区免费看

高斯課堂高數下講義pdf免費版附答案 全站導航最近更新

  • 戰壕戰爭1914國際版(Trench Warfare1914) 像素風策略戰爭游戲
  • 網易光遇手游正版 點亮星空共慶周年
  • 地鐵跑酷體驗服國際服all stars 地鐵跑酷體驗服版本
  • 六花軟件庫app手機安卓吧 超多軟件各種版本資源隨意下載。
  • 李跳跳自動跳廣告MissLee 幫你自動跳廣告
歷史搜索

熱門搜索：冒險島楓之傳說手游黎明覺醒生機騰訊正版攜程旅行app手機版地鐵跑酷手游國服逃跑吧少年官方版

首頁 → 教程素材 → 教程資料 → 高斯課堂高數下講義pdf免費版 附答案
高斯課堂高數下講義pdf免費版圖標

高斯課堂高數下講義pdf免費版附答案

  • 大小：1.2M
  • 時間：2020-11-11 10:36
  • 星級：
  • 語言：中文
  • 環境：WinAll
  • 版本：附答案
  • 類別：國產軟件/ 免費軟件
  • 官網：暫無
  • 廠商：

軟件介紹 軟件截圖 相關下載 相關文章 評論(0)

精品下載精心為您推薦：

編輯點評：

獨家的筆記整理，高斯課堂高數高分系統學習的配套講義免費分享給大家，需要備考的玩家可以對照著學習，大大的減少了花時間去整理和過程，很完整的一套講義筆記，還將重點標注起來，更易閱讀。

高斯課堂高數下講義pdf免費版

高斯課堂高數下講義pdf圖片預覽

課程目錄介紹

多元函數與重極限

偏導數與全微分

復合函數與隱函數

梯度、方向導數、多元函數極值

向量與空間幾何（一）

向量與空間幾何（二）

二重積分---直角坐標系

二重積分---極坐標系

三重積分

第一類曲線積分

第二類曲線積分

格林公式

第一類曲面積分

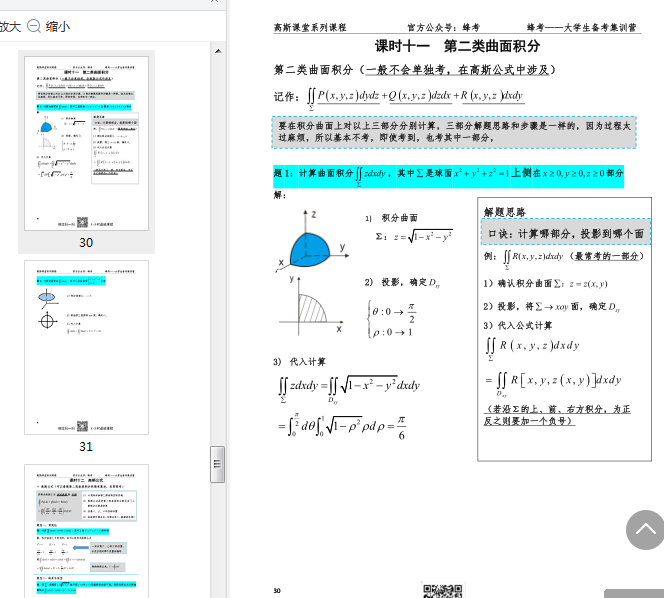
第二類曲面積分

高斯公式

常數項級數

冪級數

高數下知識點總結分享

首先我們學習了空間解析幾何。平面的三種方程適用于不同類型的題目：

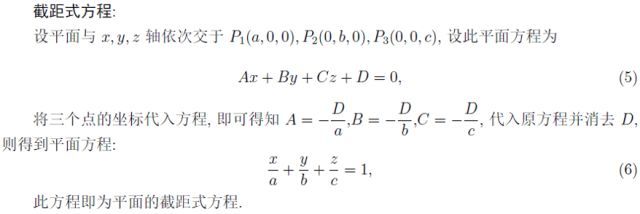
類比平面解析幾何，不難得出如下的夾角與距離的概念:

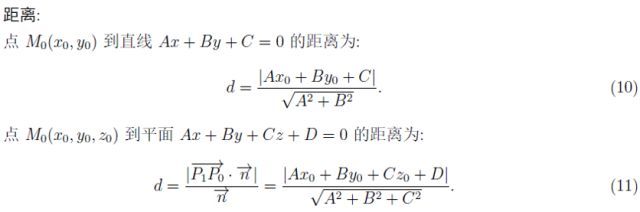
研究完平面，我們研究直線。直線也有下面三種方程:

計算夾角的方法如下:

用好過直線的平面束，可以解決很多問題:

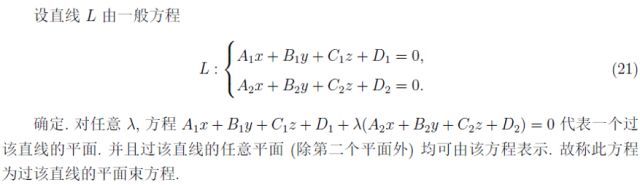
研究完直線，我們研究曲線。曲線有如下形式的一般方程:

曲線也可用參數方程表達:

我們還有投影的概念:

研究空間解析幾何，一定程度上為多元函數的研究提供了基礎，多元函數的最基本概念請同學們牢記:

隨后我們研究了偏導數:

以及高階偏導數:

用好全微分的概念，可以處理很多計算偏導數的題目:

研究完最簡單的偏導數，我們想研究復合函數的偏導數。由于復合方法多種多樣，也有如下兩種不同的情形:

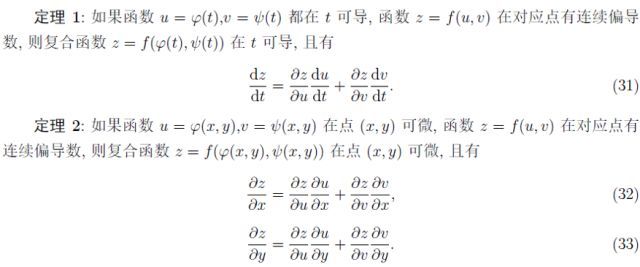
隱函數定理壓軸登場!一個方程的情形，計算偏導數的公式如下:

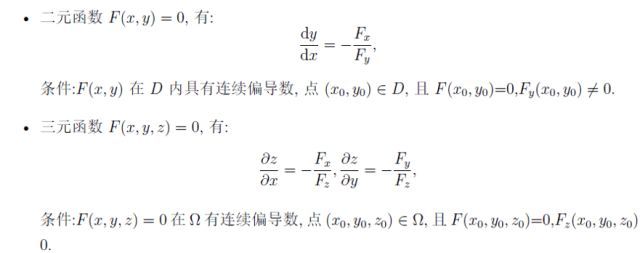
方程組聯立的情形下，我們引入了雅可比行列式的概念，方法如下。乍一看公式似乎很復雜，實際就是解一個線性方程組~

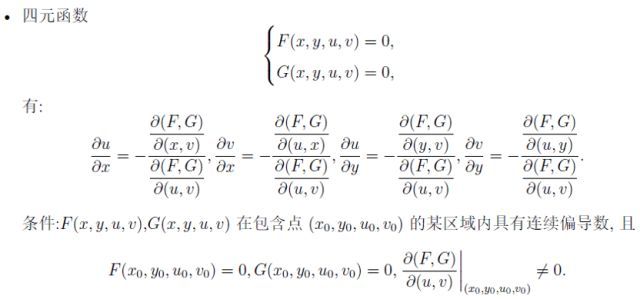
除了在坐標軸方向有偏導數，我們在任意方向都可以定義方向導數。自然要用到梯度的概念:

多元函數微分學反過來對第一章的空間解析幾何提供了方法:

在沒有限制條件的情況下，我們可以借助偏導數求出多元函數的極值:

接觸過中學數學競賽的同學會被中學數學競賽那細微的放縮以及“先猜后證”弄得暈頭轉向，而這里的拉格朗日乘子法，讓你秒殺多元條件極值問題！

上學期同學們學習了定積分、反常積分，不過有的特定的反常積分是無法用傳統方法解出來的。這就要借助我們的重積分了。類比定積分，二重積分有以下兩個性質:

如何計算重積分，可以說是高數中的關鍵部分。一般來說，我們把積分區域劃分成如下兩種區域，再進行求解，實際上，我們還是在做定積分。必要的時候，還要交換積分次序。

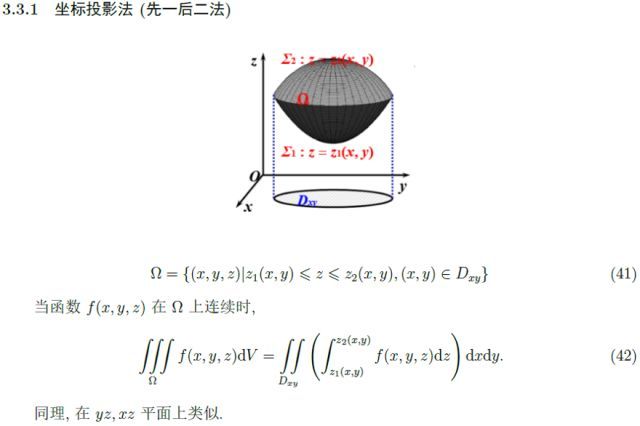
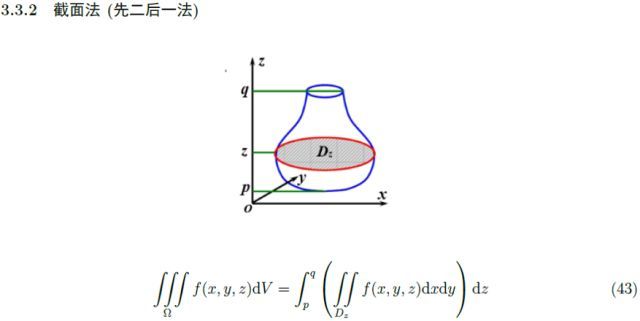
三重積分最基本的計算方法有兩種，我們的思想就是把三重積分轉化為二重積分和定積分，這兩種方法分別叫“先一后二”和“先二后一”:

當然，有時候利用對稱性，可以大大簡化問題:

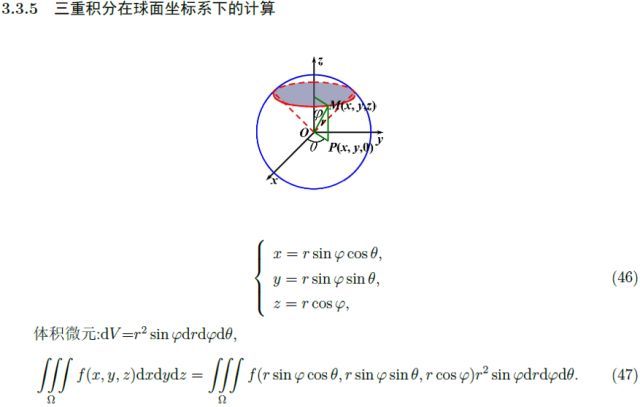
我們還介紹了柱坐標系、球坐標系，其體積元可以借助雅可比行列式計算出。這兩種坐標系常常能簡化問題，就如同二重積分中的極坐標一樣。

重積分后，我們有線、面積分:

曲線積分的一般方法如下:

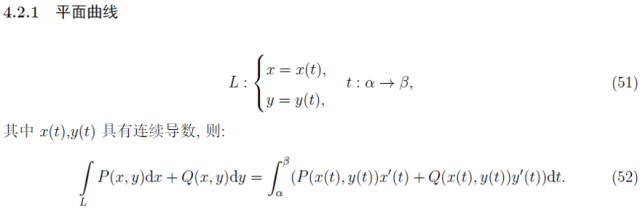
曲面積分的一般方法如下:

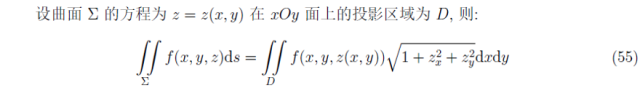
接下來是本章最重要的公式之一——格林公式及其推論:

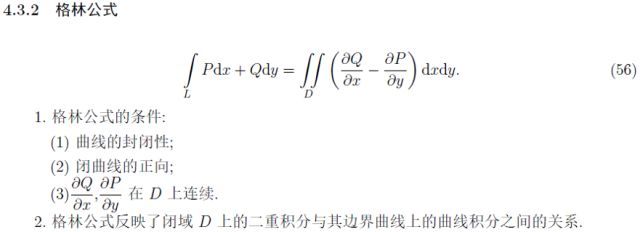
同為最重要的公式之一——高斯公式:

學期的最后，我們學習了級數的相關理論，審斂法需牢記~

我們又講了兩種重要的函數項級數——冪級數和傅里葉級數。冪級數其實同學們在學泰勒公式的時候已經接觸到了~而傅里葉級數，以三角級數擬合一般的周期函數，它的提出是一種非常偉大的想法。傅里葉級數的公式稍微復雜，請同學們記住有關公式和結論，不要弄混淆了~

高斯課堂高數下講義pdf免費版截圖

下載地址

    網友評論

    熱門評論

    最新評論

    發表評論查看所有評論(0)

    昵稱:
    表情: 高興 可 汗 我不要 害羞 好 送花 親親
    字數: 0/500 (您的評論需要經過審核才能顯示)

    TOP榜

    日本久久精品视频| 韩日美无码精品无码| 欧美精品自拍偷拍|