欢迎您访问【千度】hfqszs.com-aaaaaa级特色特黄的毛片,青青河边草高清免费,美女MM131爽爽爽,日韩欧美一区二区三区免费看

高斯課堂復(fù)變函數(shù)與積分變換講義筆記pdf免費(fèi)版 全站導(dǎo)航最近更新

  • 戰(zhàn)壕戰(zhàn)爭1914國際版(Trench Warfare1914) 像素風(fēng)策略戰(zhàn)爭游戲
  • 網(wǎng)易光遇手游正版 點(diǎn)亮星空共慶周年
  • 地鐵跑酷體驗(yàn)服國際服all stars 地鐵跑酷體驗(yàn)服版本
  • 六花軟件庫app手機(jī)安卓吧 超多軟件各種版本資源隨意下載。
  • 李跳跳自動跳廣告MissLee 幫你自動跳廣告
歷史搜索

熱門搜索：冒險(xiǎn)島楓之傳說手游黎明覺醒生機(jī)騰訊正版攜程旅行app手機(jī)版地鐵跑酷手游國服逃跑吧少年官方版

首頁 → 教程素材 → 教程資料 → 高斯課堂復(fù)變函數(shù)與積分變換講義筆記pdf免費(fèi)版
高斯課堂復(fù)變函數(shù)與積分變換講義筆記pdf免費(fèi)版圖標(biāo)

高斯課堂復(fù)變函數(shù)與積分變換講義筆記pdf免費(fèi)版

  • 大小：594KB
  • 時間：2020-11-11 11:24
  • 星級：
  • 語言：中文
  • 環(huán)境：WinAll
  • 版本：
  • 類別：國產(chǎn)軟件/ 免費(fèi)軟件
  • 官網(wǎng)：暫無
  • 廠商：

軟件介紹 軟件截圖 相關(guān)下載 相關(guān)文章 評論(0)

精品下載精心為您推薦：

編輯點(diǎn)評：

高斯課堂高數(shù)精品課程，復(fù)變函數(shù)與積分變換最新講義免費(fèi)分享，它適用大學(xué)期末考試/補(bǔ)考/重修/清考等人員，刷分還是考研，都是信手拈來，時間短，干貨滿滿，重點(diǎn)已標(biāo)記，你需要的都在這里。

課程大綱介紹

復(fù)數(shù)

復(fù)變函數(shù)

初等函數(shù)

級數(shù)

求積分

留數(shù)

利用留數(shù)求積分

Fourier傅里葉變換

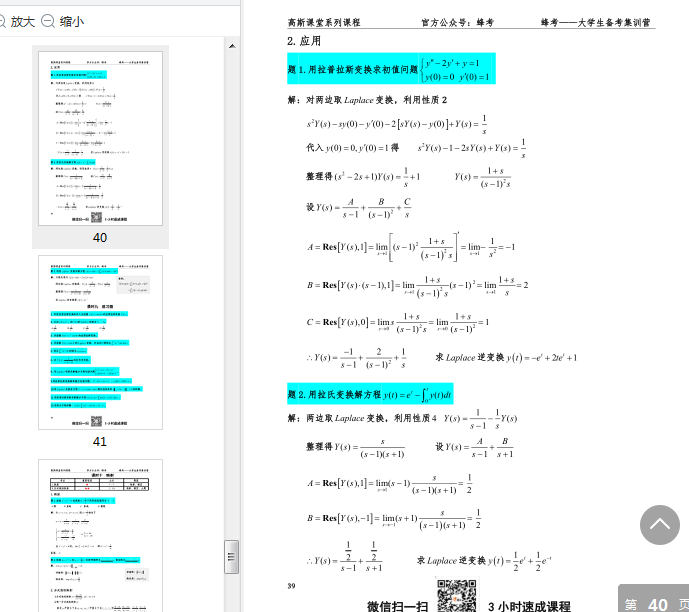
Laplace拉普拉斯變換

映射（選學(xué)）

高斯課堂復(fù)變函數(shù)與積分變換圖片預(yù)覽

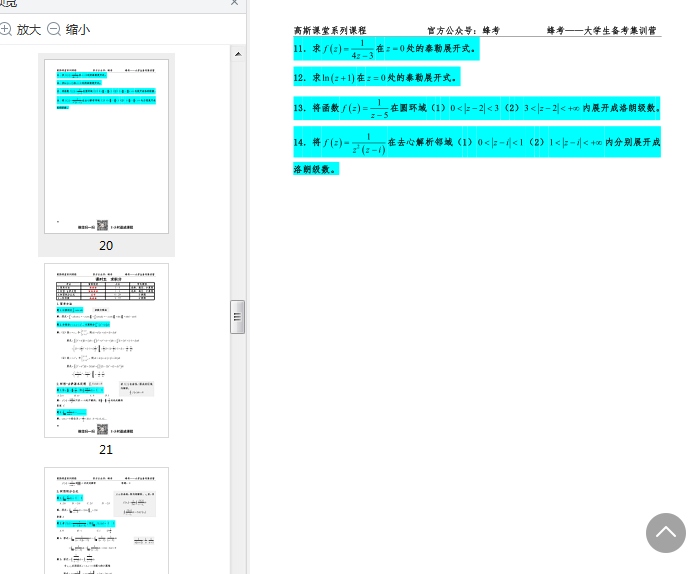
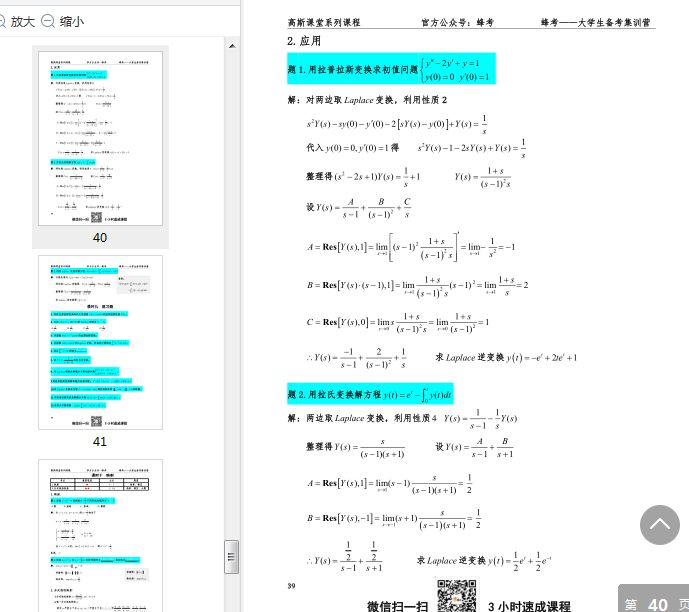
學(xué)習(xí)筆記整理

#復(fù)數(shù)及其運(yùn)算

##復(fù)數(shù)的加減乘除

復(fù)數(shù)的基礎(chǔ)知識相信大家在高中數(shù)學(xué)里已經(jīng)學(xué)過了，需要注意的是復(fù)數(shù)的乘法和除法計(jì)算比較困難，大家可以多留心記一下。

##求復(fù)數(shù)的實(shí)部與虛部

這道題的復(fù)合函數(shù)求解較難，大家可以留意一下。

##求某復(fù)數(shù)的共軛復(fù)數(shù)

求一個復(fù)數(shù)的共軛復(fù)數(shù)，只需要將他的虛部的符號變一下（原來是正號，就變成負(fù)號，原來是負(fù)號，就變成正號），就行了。

##求模，輻角和輻角主值

這些公式中arg:argumentofacomplexnumber（復(fù)數(shù)的輻角）

###求模，輻角和輻角主值的例題

輻角主值的求法比較困難，需要在坐標(biāo)上分別標(biāo)出Re和Im的值，然后將他們對應(yīng)的那個點(diǎn)與原點(diǎn)連接起來，所呈現(xiàn)出來的直線與Re軸正方向所成的夾角，就是輻角主值。

特別提醒，輻角主值的取值范圍是-180°到180°

###又一道例題

##復(fù)數(shù)的開方

大家千萬要注意，復(fù)數(shù)的開方與高中時實(shí)數(shù)的開方不一樣，16開四次方不等于2，而需要用到專門的復(fù)數(shù)開方公式。在計(jì)算完成之后，記得加上K=0，1,2，3，……n-1;千萬千萬要記得，不是n,不是n,不是n,重要的事情說三遍。

##代數(shù)式，三角式，指數(shù)式轉(zhuǎn)換。

重點(diǎn)知識整理

第一章：復(fù)數(shù)與復(fù)變函數(shù)

所謂復(fù)變函數(shù)，就是自變量為復(fù)數(shù)的函數(shù)。

研究主要對象是某種意義下可導(dǎo)的復(fù)變函數(shù)，稱為解析函數(shù)。

知識點(diǎn)層次為：復(fù)數(shù)->復(fù)變函數(shù)->復(fù)變函數(shù)性質(zhì)->初等解析函數(shù)及性質(zhì)

復(fù)數(shù)代數(shù)式：z=x+iy

復(fù)數(shù)三角式：z=r(cosθ+isinθ)

歐拉公式：eiθ=cosθ+isinθ

指數(shù)式：z=reiθ

主值　：θ=argz=arctan(y/x)

棣莫弗公式：(cosθ+isinθ)n=cosnθ+isinnθ

解析函數(shù)

復(fù)變函數(shù)可導(dǎo)的條件：實(shí)部虛部兩個二元函數(shù)可微，實(shí)部與虛部通過C-R條件聯(lián)系起來。

若函數(shù)f(z)在z0某一領(lǐng)域處處可導(dǎo)，稱f(z)在z0處解析。

若f(z)在區(qū)域E內(nèi)每一點(diǎn)解析，稱f(z)是E內(nèi)的一個解析函數(shù)。

f在E內(nèi)解析的充要條件是，u、v在E內(nèi)任一點(diǎn)可微，且滿足C-R條件。

第二章　復(fù)變函數(shù)和積分

復(fù)變函數(shù)積分

柯西積分

解析函數(shù)與調(diào)和函數(shù)的關(guān)系

線積分與路徑無關(guān)等價于該函數(shù)沿單連域中任何閉曲線的積分為零。

柯西積分定理：單連域內(nèi)解析積分為零。

如果函數(shù)f(z)在單連域E內(nèi)解析，那么積分　只與起點(diǎn)與終點(diǎn)有關(guān)，與連接點(diǎn)和終點(diǎn)的路徑無關(guān)。

由于復(fù)變函數(shù)的積分為沿著有向曲線的積分，可以通過二元函數(shù)關(guān)于坐標(biāo)的曲線積分式來獲得。

若已知曲線的參數(shù)方程，則復(fù)變函數(shù)可以化為定積分計(jì)算，這時只要將被積函數(shù)f(z)的變量z換為z(t)=x(t)+iy(t),將dz換為　z'(t)dt即可。

對于解析函數(shù)的積分，由于積分與路徑無關(guān)，可以通過與牛頓萊布尼茲公式相同來計(jì)算。

至于計(jì)算沿封閉路線的積分，往往以柯西積分定理、復(fù)合閉路定理、閉路變形公式、柯西積分公式、高階導(dǎo)數(shù)公式為工具。

滿足拉普拉斯方程，且具有二階連續(xù)偏導(dǎo)的函數(shù)稱為調(diào)和函數(shù)。

任何一個在區(qū)域E上解析的函數(shù)f(z)=u(x,y)+iv(x,y),其實(shí)部與虛部都是該區(qū)域上的調(diào)和函數(shù)。

如果u(x,y)是區(qū)域E內(nèi)的調(diào)和函數(shù)，則存在一個v(x,y)使u+iv在E內(nèi)解析。

第三章　級數(shù)

一個函數(shù)的解析性與該函數(shù)能否級數(shù)展開是等價的。

羅朗級數(shù)

對于一般復(fù)數(shù)列的討論可以歸結(jié)為對兩個實(shí)數(shù)列的討論。

對于一般復(fù)數(shù)項(xiàng)級數(shù)的討論可以歸結(jié)為對實(shí)數(shù)項(xiàng)級數(shù)的討論。

復(fù)變函數(shù)項(xiàng)級數(shù)：f1(z)+f2(z)+....+fn(z)+...

冪級數(shù)是一種特殊復(fù)變函數(shù)項(xiàng)級數(shù)。以cn(z-z0)n為一般項(xiàng)。

冪級數(shù)與解析函數(shù)有密切關(guān)系：

冪級數(shù)在一定區(qū)域內(nèi)收斂于一個解析函數(shù)

一個解析函數(shù)在其解析點(diǎn)的領(lǐng)域內(nèi)能展開成冪級數(shù)。

阿貝爾定理　　收斂圓和收斂半徑

達(dá)朗貝爾公式

柯西公式

在收斂圓內(nèi)，冪級數(shù)和和函數(shù)是解析函數(shù)。即，任何一個收斂半徑大于零的冪級數(shù)在其收斂圓內(nèi)代表一個解析函數(shù)。

泰勒定理　　能展成冪級數(shù)

f(z)在區(qū)域E內(nèi)解析的充要條件是　f(z)　在E內(nèi)任一點(diǎn)z0的領(lǐng)域內(nèi)可以馬爾代展成(z-z0)的冪級數(shù)，即泰勒級數(shù)。

如果z=z0是f(z)的奇點(diǎn)，那么在奇點(diǎn)的領(lǐng)域內(nèi)就不能展開成泰勒級數(shù)。

羅朗級數(shù)

第四章　留數(shù)理論

孤立奇點(diǎn)的分類和性質(zhì)

留數(shù)的求法

用留數(shù)定理計(jì)算實(shí)函數(shù)積分和無窮限廣義積分

如果f(z)在　z0點(diǎn)去心領(lǐng)域內(nèi)解析，而z0點(diǎn)不解析，稱z0為f(z)的孤立奇點(diǎn)。

如果f(z)在z0點(diǎn)的主要部分全部等于零，稱z0為f(z)的可去奇點(diǎn)

如果f(z)在z0點(diǎn)的主要部分只有有限項(xiàng)m,　稱z0為f(z)的m級極點(diǎn)。

如果f(z)在z0點(diǎn)的主要部分有無窮多項(xiàng)，稱z0為f(z)的本性奇點(diǎn)。

可去奇點(diǎn)判定　如果z0為f(z)的孤立奇點(diǎn)，下列三個條件是等價的：

f(z)在z0點(diǎn)的主要部分為零。

limf(z)存在。

f(z)　在點(diǎn)z0的某去心領(lǐng)域有界

m級極點(diǎn)的判定　如果z0為f(z)的孤立奇點(diǎn)，下列三個條件等價：

f(z)在z0點(diǎn)的主要部分為

f(z)在點(diǎn)z0的某去心領(lǐng)域內(nèi)能表示成

g(z)=1/f(z)以z0　為m級零點(diǎn)

留數(shù)定理　把沿封閉曲線積分的整體問題，化為計(jì)算其各孤立奇點(diǎn)處留數(shù)的局部問題。

留數(shù)求法

可去奇點(diǎn)：若z0為f(z)的可去，面積分Res{f(z),z0}=0.

極點(diǎn)：

本性奇點(diǎn)：通過羅朗展開式來求留數(shù)。

第五章　保角映射

映射的旋轉(zhuǎn)角不變性　解析函數(shù)的導(dǎo)數(shù)幅角的幾何意義。

映射的保角性　映射具有保持兩曲線間夾角的大小與方向不變的特性。　

伸縮率的不變性　當(dāng)z0取定后，伸縮率|f'(z0)|是確定的，從而與過點(diǎn)z0的曲線C的選擇無關(guān)。　

保角映射　設(shè)w=f(z)在z0的領(lǐng)域內(nèi)有定義，若映射　w=f(z)在點(diǎn)z0　有保角性（大小、方向不變）和伸縮率不變性，稱映射w在點(diǎn)z0是保角的，或w=f(z)在z0處是保角映射。

若　w=f(z)在區(qū)域E內(nèi)解析，則它在E內(nèi)導(dǎo)數(shù)不為零的點(diǎn)處是保角的。

上述保角映射不僅保持曲線夾角的大小不變而且夾角的方向不變。僅保持夾角的絕對值不變而方向相反的映射稱為第二類保角映射。

分式線性映射　

任何一個分式線性映射可由兩種典型的映射復(fù)合而成。

分式線性映射在擴(kuò)充的復(fù)平面上是一一對應(yīng)的，具有保圓性的保角映射。

這里的保圓性是指：在分式線性映射下，將圓周（直線）映射成圓周（直線）。

也就是說，如果給定的圓周或直線上沒有點(diǎn)映射或者無窮遠(yuǎn)點(diǎn)，那么它就映射成半徑為有限的圓周，如果有一點(diǎn)映射成無窮遠(yuǎn)點(diǎn)，那么它就映射成直線。

分式線性映射除了保圓性之外，還有保對稱性。

三種重要的分式線性映射：上半平面映射上半平面，上半平面映射單位圓域，單位圓域映射成單位圓域。

高斯課堂復(fù)變函數(shù)與積分變換講義筆記pdf免費(fèi)版截圖

下載地址

    網(wǎng)友評論

    熱門評論

    最新評論

    發(fā)表評論查看所有評論(0)

    昵稱:
    表情: 高興 可 汗 我不要 害羞 好 送花 親親
    字?jǐn)?shù): 0/500 (您的評論需要經(jīng)過審核才能顯示)

    TOP榜

    色婷婷六月亚洲婷婷丁香| 色色色色色五月丁香婷婷| 免费激情网站|